AGD

Adpative step-size

Considering a cost functional with the same characteristics as the one used for the GD case, then

Problem (1)

• augment the hyperFunGD class by implementing some adpative step-size methods:

  • Cauchy step-size.

  • Barzilai-Borwein (BB), all three versions.

  • Cauchy-BB.

Recall

When solving the GD simulation, the following classes / routines were considered

• class ss (step-size)

  
  

  from enum import Enum, IntEnum, unique
  
  

  @unique
  class ss(Enum):
    Cte            = (0, 'Cte step-size')
    Cauchy         = (1, 'Cauchy')
    CauchyLagged   = (2, 'Cauchy-BB (lagged)')
    BBv1           = (6, 'BBv1')
    BBv2           = (7, 'BBv2')
    BBv3           = (8, 'BBv3')
  
    def __init__(self, val, txt):
        self.val  = val
        self.txt  = txt
  
    @classmethod
    def printSS(cls):
        for k in cls:
          print('ss.{}:'.format(k.name), k.val, k.txt)
  

• class hyperFun

  
  

Cauchy

Given the cost functional \(\displaystyle f(\mathbf{u}) = 0.5\| \Phi \mathbf{u} - \mathbf{b} \|_2^2 \) the Cauchy step-size is computed via (among others, see [Yua08])

\[\begin{eqnarray*} \alpha & = & \frac{\| \mathbf{g} \|_2^2}{ \| \Phi \mathbf{g} \|_2^2 }, \end{eqnarray*}\]

where \(\mathbf{g} = \nabla f(\mathbf{u})\).

BB

Given the cost functional \(\displaystyle f(\mathbf{u})\) and the vectors \(\mathbf{s}_k\) and \(\mathbf{y}_k\), where \( \begin{array}{ll} \bullet & \mathbf{s}_k = \mathbf{u}_k - \mathbf{u}_{k-1}. \\ \bullet & \mathbf{y}_k = \mathbf{g}_k - \mathbf{g}_{k-1}. \\ \bullet & \mathbf{u}_k \mbox{ is the solution at iteration }k. \\ \bullet & \mathbf{g}_k =\nabla f(\mathbf{u}_k) \end{array} \)

then (see [BB88] and [LW19] )

\[\begin{split}\begin{array}{rcll} \alpha_{1} & = & \displaystyle \frac{\| \mathbf{s}_k \|_2^2}{ \langle \mathbf{s}_k, \mathbf{y}_k\rangle } & \qquad \color{darkgray}\mbox{labeled ``BBv1''}\\ & & \\ \alpha_{2} & = & \displaystyle \frac{\langle \mathbf{s}_k, \mathbf{y}_k\rangle }{\| \mathbf{y}_k \|_2^2} & \qquad \color{darkgray}\mbox{labeled ``BBv2''} \\ & & \\ \alpha_{3} & = & \displaystyle \sqrt{ \alpha_1 \cdot \alpha_2 } & \\ & = & \displaystyle \frac{ \| \mathbf{s}_k \|_2 }{\| \mathbf{y}_k \|_2} & \qquad \color{darkgray}\mbox{labeled ``BBv3''} \end{array} \end{split}\]

Cauchy-BB

This method is also called Cauchy ``lagged’’: Given the cost functional \(\displaystyle f(\mathbf{u})\) and initial solution \(\mathbf{x}_0\), then (see [RS02])

\(\begin{array}{l} \mbox{for } k = 0,\,1,\, \ldots \\ \begin{array}{lll} & \mbox{if } REM(\,(k,\,2) == 0 & \end{array} \\ \begin{array}{lll} & & \alpha_k = \alpha_{k}^{\mbox{C}} \qquad\qquad{\color{lightgray} \mbox{ Cauchy step-size}} \\ \end{array} \\ \begin{array}{lll} & \mbox{else} \end{array} \\ \begin{array}{lll} & & \alpha_k = \alpha_{k\mbox{-}1} \qquad\qquad{\color{lightgray} \mbox{BB}} \\ \end{array} \\ \begin{array}{lll} & \\ & \mathbf{x}_{k\mbox{+}1} = \mathbf{x}_{k} - \alpha_k \nabla \mathbf{f}_{k} \\ \end{array} \\ \end{array} \)

Proposed solution

Among other pausible alternatives, and assuming the optimization problem is given by \(F(\mathbf{u}_k) = f( \mbox{fwOp}(\mathbf{u}_k), b)\), where

• g: variable that represents \(\mathbf{g}_k = \nabla F(\mathbf{u}_k)\),

• self.fwOp(g) computes \(f( \mbox{fwOp}(\mathbf{g}_k), b)\),

the considered adaptive step-size methods may be written as

Cauchy

    def ssCauchy(self, u, alpha, k, g):

        num = g.ravel().dot( g.ravel() )
        z   = self.fwOp(g)

        return num/z.ravel().dot( z.ravel() )

BB

    def ssBBv1(self, u, alpha, k, g):

        if k == 0: # Cauchy randSol

           self.uPrv = u.ravel().copy()
           self.gPrv = g.ravel().copy()

           num = g.ravel().dot( g.ravel() )
           z   = self.fwOp(g)

           self.alphaBBv1 = num/z.ravel().dot( z.ravel() )

        else:

           s = u.ravel() - self.uPrv
           y = g.ravel() - self.gPrv

           self.alphaBBv1 = s.dot(s) / s.dot(y)

           self.uPrv = u.ravel().copy()     # records previous solution
           self.gPrv = g.ravel().copy()

        return  self.alphaBBv1


    def ssBBv2(self, u, alpha, k, g):

        if k == 0: # Cauchy randSol

           self.uPrv = u.ravel().copy()
           self.gPrv = g.ravel().copy()

           num = g.ravel().dot( g.ravel() )
           z   = self.fwOp(g)

           self.alphaBBv2 = num/z.ravel().dot( z.ravel() )

        else:

           s = u.ravel() - self.uPrv
           y = g.ravel() - self.gPrv

           self.alphaBBv2 = s.dot(y) / y.dot(y)

           self.uPrv = u.ravel().copy()     # records previous solution
           self.gPrv = g.ravel().copy()

        return  self.alphaBBv2


    def ssBBv3(self, u, alpha, k, g):

        if k == 0: # Cauchy randSol

           self.uPrv = u.ravel().copy()
           self.gPrv = g.ravel().copy()

           num = g.ravel().dot( g.ravel() )
           z   = self.fwOp(g)

           self.alphaBBv3 = num/z.ravel().dot( z.ravel() )

        else:

           s = u.ravel() - self.uPrv
           y = g.ravel() - self.gPrv

           self.alphaBBv3 = np.sqrt( s.dot(s) / y.dot(y) )

           self.uPrv = u.ravel().copy()     # records previous solution
           self.gPrv = g.ravel().copy()

        return  self.alphaBBv3

Cauchy-BB

    def ssCauchyLagged(self, u, alpha, k, g):

        if np.remainder(k,2) == 0:
           num = g.ravel().dot( g.ravel() )
           z   = self.fwOp(g)
           self.alphaCL = num/z.ravel().dot( z.ravel() )

        return self.alphaCL

---

Simulation

1. Generate input data

    import numpy as np

    # --- Data generation (N,M: user inputs)
    # --------------------------------------
    rng = np.random.default_rng()

    A = rng.normal(size=[N,M])
    D = np.sqrt(max(N,M))*np.diag( rng.random([max(N,M),]), 0)
    A += D[0:N,0:M]
    A /= np.linalg.norm(A,axis=0)

    xOrig = np.random.randn(M,1)

    b = A.dot(xOrig) + sigma*np.random.randn(N,1)

2. Load the optimization problem

    # --- Optimization model
    # --- (see "Parameters", "OptProb", "E.g. quadratic func."
    #      in the tabbed panel above)
    # ---------------------------------------------------------

    OptProb = hosgdFunQlin(A,b)

3. Select the adaptive step-size method

    # --- It is assumed that class 'ss' is defined
    #     in file 'HoSGDdefs.py'
    # --- (see "Parameters", "hyperFun", "class ss"
    #      in the tabbed panel above)
    # ---------------------------------------------------------

    import HoSGDdefs as hosgdDef


    # --- hyperPars
    # --- (see "Parameters", "hyperFun", "E.g."
    #      in the tabbed panel above)
    # ---------------------------------------------------------

    # Cte. SS:
    hyperP = hosgdHyperFun(OptProb, ssPolicy=hosgdDef.ss.Cte)

    # Cauchy SS:
    hyperP_C = hosgdHyperFun(OptProb, ssPolicy=hosgdDef.ss.Cauchy)

    # Cauchy BBv1 SS:
    hyperP_BB1 = hosgdHyperFun(OptProb, ssPolicy=hosgdDef.ss.BBv1)

    # Cauchy-BB SS:
    hyperP_CBB = hosgdHyperFun(OptProb, ssPolicy=hosgdDef.ss.CauchyLagged)

    # etc.

4. Execute GD + adaptive SS

    # --- nIter, alpha0: user defined.
    # --- OptProb: see #2 in the current list
    # --- hyperP / ssPolicy: see #3 in the current list

    # Cte. SS:
    u, stats = hosgdGD(OptProb, nIter, alpha, hyperP)

    # Cauchy SS:
    u1, stats1 = hosgdGD(OptProb, nIter, alpha, hyperP_C)

    # Cauchy BBv1:
    u2, stats2 = hosgdGD(OptProb, nIter, alpha, hyperP_BB1)

    # Cauchy-BB SS:
    u3, stats3 = hosgdGD(OptProb, nIter, alpha, hyperP_CBB)

---

Full solution

HoSGDdefs.py

from enum import Enum, IntEnum, unique

@unique
class ss(Enum):
  Cte            = (0, 'Cte step-size')
  Cauchy         = (1, 'Cauchy')
  CauchyLagged   = (2, 'Cauchy-BB (lagged)')
  BBv1           = (6, 'BBv1')
  BBv2           = (7, 'BBv2')
  BBv3           = (8, 'BBv3')

  def __init__(self, val, txt):
      self.val  = val
      self.txt  = txt

  @classmethod
  def printSS(cls):
      for k in cls:
        print('ss.{}:'.format(k.name), k.val, k.txt)

HoSGDL2gd.py

import numpy as np
import scipy as sc
from scipy import signal

import matplotlib.pylab as PLT

import HoSGDdefs as hosgdDef
from HoSGDdefs import hosgdOptProb



class hosgdHyperFun(object):
    r"""Class related to routines associated to hyperPars computation
    """

    def __init__(self, OptProb, ssPolicy=hosgdDef.ss.Cte):
        self.ssPolicy = ssPolicy
        self.fwOp = OptProb.fwOp
        self.SS   = self.sel_SS()

    def sel_SS(self):
      switcher = {
          hosgdDef.ss.Cte.val:          self.ssCte,
          hosgdDef.ss.Cauchy.val:       self.ssCauchy,
          hosgdDef.ss.CauchyLagged.val: self.ssCauchyLagged,
          hosgdDef.ss.BBv1.val:         self.ssBBv1,
          hosgdDef.ss.BBv2.val:         self.ssBBv2,
          hosgdDef.ss.BBv3.val:         self.ssBBv3,
          }

      ssFun = switcher.get(self.ssPolicy.val, "nothing")

      func = lambda u, alpha, k, g: ssFun(u, alpha, k, g)

      return func

    # --- === ---

    def ssCte(self, u, alpha, k, g):
        return alpha


    def ssCauchy(self, u, alpha, k, g):

        num = g.ravel().dot( g.ravel() )
        z   = self.fwOp(g)

        return num/z.ravel().dot( z.ravel() )



    def ssCauchyLagged(self, u, alpha, k, g):

        if np.remainder(k,2) == 0:
           num = g.ravel().dot( g.ravel() )
           z   = self.fwOp(g)
           self.alphaCL = num/z.ravel().dot( z.ravel() )

        return self.alphaCL


    def ssBBv1(self, u, alpha, k, g):

        if k == 0: # Cauchy randSol

           self.uPrv = u.ravel().copy()
           self.gPrv = g.ravel().copy()

           num = g.ravel().dot( g.ravel() )
           z   = self.fwOp(g)

           self.alphaBBv1 = num/z.ravel().dot( z.ravel() )

        else:

           s = u.ravel() - self.uPrv
           y = g.ravel() - self.gPrv

           self.alphaBBv1 = s.dot(s) / s.dot(y)

           self.uPrv = u.ravel().copy()     # records previous solution
           self.gPrv = g.ravel().copy()

        return  self.alphaBBv1


    def ssBBv2(self, u, alpha, k, g):

        if k == 0: # Cauchy randSol

           self.uPrv = u.ravel().copy()
           self.gPrv = g.ravel().copy()

           num = g.ravel().dot( g.ravel() )
           z   = self.fwOp(g)

           self.alphaBBv2 = num/z.ravel().dot( z.ravel() )

        else:

           s = u.ravel() - self.uPrv
           y = g.ravel() - self.gPrv

           self.alphaBBv2 = s.dot(y) / y.dot(y)

           self.uPrv = u.ravel().copy()     # records previous solution
           self.gPrv = g.ravel().copy()

        return  self.alphaBBv2


    def ssBBv3(self, u, alpha, k, g):

        if k == 0: # Cauchy randSol

           self.uPrv = u.ravel().copy()
           self.gPrv = g.ravel().copy()

           num = g.ravel().dot( g.ravel() )
           z   = self.fwOp(g)

           self.alphaBBv3 = num/z.ravel().dot( z.ravel() )

        else:

           s = u.ravel() - self.uPrv
           y = g.ravel() - self.gPrv

           self.alphaBBv3 = np.sqrt( s.dot(s) / y.dot(y) )

           self.uPrv = u.ravel().copy()     # records previous solution
           self.gPrv = g.ravel().copy()

        return  self.alphaBBv3


# ===========================================

class hosgdFunQlin(hosgdOptProb):
    r""" 0.5|| Au - b ||_2^2

    """

    def __init__(self, A, b, gNormOrd=2, Nstats=4, verbose=10, initSol=None):

        self.A = A
        self.b = b
        self.gNormOrd = gNormOrd
        self.Nstats   = Nstats
        self.verbose  = verbose
        self.initSol  = initSol      #  if not None --> reproducible initial solution

    # ---------


    # ---------

    def costFun(self, u):

        return 0.5*np.linalg.norm( self.A.dot(u).ravel()-self.b.ravel(), ord=2)**2


    # ---------

    def fwOp(self, u):

        return self.A.dot(u)

    # ---------

    def gradFun(self, u):

        return self.A.transpose().dot(self.A.dot(u) - self.b)

    # ---------

    def randSol(self):

        if self.initSol is None:
           rng = np.random.default_rng()
        else:
           rng = np.random.default_rng(self.initSol)

        return rng.normal(size=[self.A.shape[1],1])


    # ---------

    def computeStats(self, u, alpha, k, g):

        cost  = self.costFun(u)

        gNorm = self.gradNorm(g, self.gNormOrd)

        return np.array([k, cost, alpha, gNorm])


    def printStats(self, k, nIter, v):

        if k == 0:
            print('\n')

        if self.verbose > 0:

            if np.remainder(k,self.verbose)==0 or k==nIter-1:
               print('{:>3d}\t {:.3e}\t {:.2e}    {:.2e}'.format(int(v[k,0]),v[k,1],v[k,2],v[k,3]))

        return

    def gradNorm(self, g, ord=2):

        if g is None:
           return -1.0

        if ord == 2:
            return np.linalg.norm(g.ravel(),ord=ord)**ord
        else:
            return np.linalg.norm(g.ravel(),ord=ord)

# ===========================================


def hosgdGD(OptProb, nIter, alpha0, hyperFun):

    u = OptProb.randSol()
    stats = np.zeros( [nIter, OptProb.Nstats] )

    for k in range(nIter):

        g     = OptProb.gradFun(u)

        alpha = hyperFun.SS(u, alpha0, k, g)

        u = u - alpha*g

        stats[k,:] = OptProb.computeStats(u, alpha, k, g)

        OptProb.printStats(k, nIter, stats)

    return u, stats




def exQlin(nIter, alpha, N=1000, M=500, sigma=0.05, ssPolicy=hosgdDef.ss.Cte):

    # Examples
    # u, st = H.exQlin(40, np.array([0.05, 0.01, 0.001]), N=500, M=2000, ssPolicy=H.hosgdDef.ss.Cte)

    # --- Data generation
    # -------------------
    rng = np.random.default_rng()

    A = rng.normal(size=[N,M])
    D = np.sqrt(max(N,M))*np.diag( rng.random([max(N,M),]), 0)
    A += D[0:N,0:M]
    A /= np.linalg.norm(A,axis=0)

    xOrig = np.random.randn(M,1)

    b = A.dot(xOrig) + sigma*np.random.randn(N,1)

    # --- Optimization model
    # ----------------------

    OptProb = hosgdFunQlin(A,b)

    # --- HyperPar
    # ------------

    if isinstance(ssPolicy, list):

        u = []
        stats = []
        ssPlcyList = []
        alphaList = []

        for n in range(len(ssPolicy)):
            hyperP = hosgdHyperFun(OptProb, ssPolicy=ssPolicy[n])


            sol = hosgdGD(OptProb, nIter, alpha, hyperP)
            u.append(sol[0])
            stats.append(sol[1])
            ssPlcyList.append( ssPolicy[n] )

            alphaList.append(alpha)

        stDict = {'stats': stats, 'ssPlcy': ssPlcyList, 'alphaVal': alphaList, 'alphaPlot':True}

        plotGDDictStats(stDict)

    else:
      hyperP = hosgdHyperFun(OptProb, ssPolicy=ssPolicy)

      # --- Call GD
      # -----------
      u, stats = runGD(OptProb, nIter, alpha, hyperP, ssPolicy)

    return u, stats



def runGD(OptProb, nIter, alpha, hyperP, ssPolicy):

      if hasattr(alpha, "shape"):

        u = []
        stats = []
        ssPlcyList = []

        for n in range(alpha.shape[0]):
            sol = hosgdGD(OptProb, nIter, alpha[n], hyperP)
            u.append(sol[0])
            stats.append(sol[1])

            if isinstance(ssPolicy, list):
               ssPlcyList.append( ssPolicy[n] )
               flagAlphaPlot = True
            else:
               ssPlcyList.append( ssPolicy )
               flagAlphaPlot = False

        stDict = {'stats': stats, 'ssPlcy': ssPlcyList, 'alphaVal': alpha, 'alphaPlot':flagAlphaPlot}

        plotGDDictStats(stDict)


      else:

        u, stats = hosgdGD(OptProb, nIter, alpha, hyperP)

        plotGDStats(stats, ssPolicy)


      return u, stats


def plotGDStats(stats, ssPolicy):

  # --- Plot results ---
  PLT.figure()
  PLT.plot(stats[:,1], label=r'$\alpha_k$ : {0}'.format(ssPolicy.txt) )
  PLT.legend(loc='upper right')
  PLT.ylabel(r'$f(x) = \frac{1}{2}\| A \mathbf{x} - \mathbf{b} \|_2^2$', fontsize=16)
  PLT.xlabel('Iteration', fontsize=16)

  if ssPolicy.val > 0:

    PLT.figure()
    PLT.plot(stats[1::,2], label=r'$\alpha_k$ : {0}'.format(ssPolicy.txt) )
    PLT.legend(loc='upper right')
    PLT.ylabel(r'$\alpha$', fontsize=20)
    PLT.xlabel('Iteration', fontsize=16)

  PLT.show()


def plotGDDictStats(stDict):


  stats  = stDict.get('stats')
  ssPlcy = stDict.get('ssPlcy')
  alpha  = stDict.get('alphaVal')

  alphaPlot  = stDict.get('alphaPlot')

  # --- Plot cost function ---
  PLT.figure()

  for n in range(len(stats)):
    PLT.semilogy(stats[n][:,1], label=r'$\alpha_k$ : {0} -- {1}'.format(alpha[n], ssPlcy[n].txt) )

  PLT.legend(loc='upper right')
  PLT.ylabel(r'$f(x) = \frac{1}{2}\| A \mathbf{x} - \mathbf{b} \|_2^2$', fontsize=16)
  PLT.xlabel('Iteration', fontsize=16)
  PLT.title('Cost functional',fontsize=16)

  # --- Plot SS ---
  if alphaPlot:

    PLT.figure()

    for n in range(len(stats)):
      PLT.plot(stats[n][1::,2], label=r'$\alpha_k$ : {0}'.format(ssPlcy[n].txt) )

    PLT.legend(loc='upper right')
    PLT.ylabel(r'$\alpha$', fontsize=20)
    PLT.xlabel('Iteration', fontsize=16)
    PLT.title('Step-size',fontsize=16)

  # ---

  # --- Plot gradNorm ---
  if False:
    PLT.figure()

    for n in range(len(stats)):
      PLT.semilogy(stats[n][1::,3], label=r'$\alpha_k$ : {0}'.format(ssPlcy[n].txt) )

    PLT.legend(loc='upper right')
    PLT.ylabel(r'$\| \nabla F \|_2$', fontsize=20)
    PLT.xlabel('Iteration', fontsize=16)
    PLT.title('Gradient norm',fontsize=16)

  # ---

  PLT.show()

Simple Simulation

import numpy as np
import HoSGDlabGD as H
import HoSGDdefs as hosgdDef

# set different ssPolicies
ssPolicy = []
ssPolicy.append( hosgdDef.ss.Cte )
ssPolicy.append( hosgdDef.ss.Cauchy )
ssPolicy.append( hosgdDef.ss.CauchyLagged )
ssPolicy.append( hosgdDef.ss.BBv1 )
ssPolicy.append( hosgdDef.ss.BBv2 )

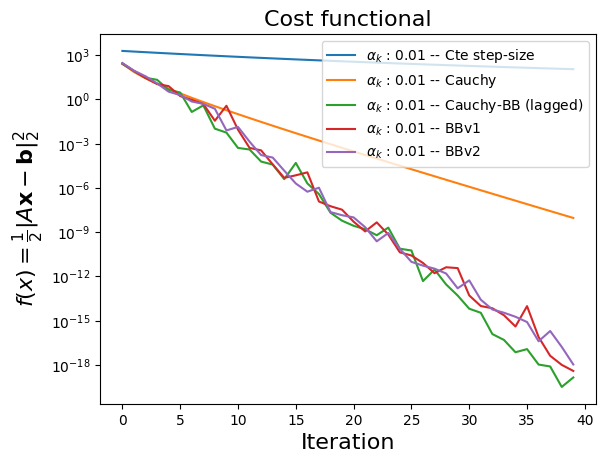
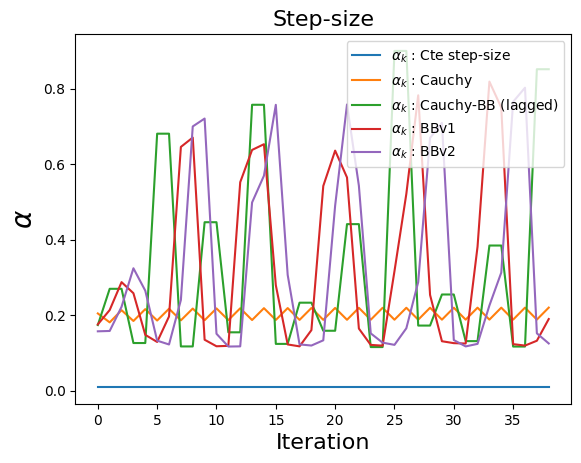
u, st = H.exQlin(40, 0.01, N=500, M=2000, ssPolicy=ssPolicy)

---

---

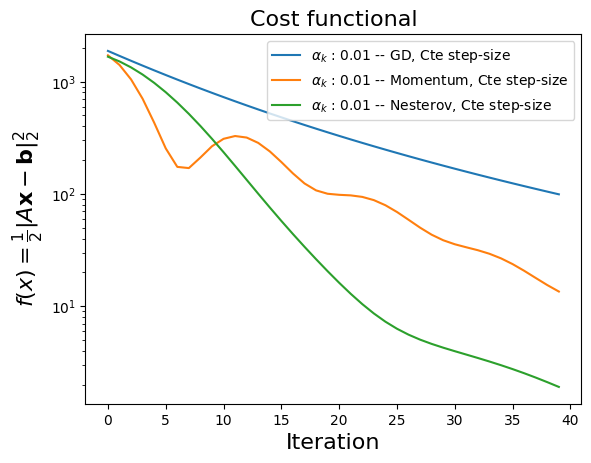
Accelerted GD: Momentum & Nesterov

Problem (2)

• implement two accelerated versions of GD, namely

  • Momentum (a.k.a. Polyak’s heavy ball, see [Pol64]) acceleration.

  • Nesterov acceleration [Nes83].

Momentum

Given the cost functional \(\displaystyle F(\mathbf{u}) = f(\mbox{Op}(\mathbf{u}), \mathbf{b}) \) and parameter \(\gamma\) then

\[\begin{split} \begin{array}{lcl} % \phantom{Momentum}\mbox{GD} & : & \begin{array}{rcl}\mathbf{u}_{k+1} & = & \mathbf{u}_{k} - \alpha \cdot \nabla F(\mathbf{u}_{k}) \end{array} \\ % & & \\ % \phantom{GD}\mbox{Momentum} & : & \begin{array}{rcl} \mathbf{z}_{k+1} & = & \gamma\cdot\mathbf{z}_{k} - \alpha \cdot \nabla F(\mathbf{u}_{k}) \\ \mathbf{u}_{k+1} & = & \mathbf{u}_{k} + \mathbf{z}_{k+1} \end{array} \\ \end{array} \end{split}\]

Nesterov

Given the cost functional \(\displaystyle F(\mathbf{u}) = f(\mbox{Op}(\mathbf{u}), \mathbf{b}) \) and the inertial sequence \(\{ \gamma_k \}\) then

\[\begin{split} \begin{array}{lcl} % \phantom{Nesterov}\mbox{GD} & : & \begin{array}{rcl}\mathbf{u}_{k+1} & = & \mathbf{u}_{k} - \alpha \cdot \mathbf{g}_k \end{array} \\ % & & \\ % \phantom{GD}\mbox{Nesterov} & : & \begin{array}{rcl} \mathbf{u}_{k+1} & = & \mathbf{y}_{k} - \alpha \cdot \nabla F(\mathbf{y}_{k}) \\ \mathbf{y}_{k+1} & = & \mathbf{u}_{k} + \gamma_k\cdot(\mathbf{u}_{k+1} - \mathbf{u}_{k}) \end{array} \\ \end{array} \end{split}\]

Proposed solution

Among other pausible alternatives, the considered accelerated GD algorithms may be written as

Momentum

Highlighted lines point out the differences between GD and Momentum [Pol64].

def hosgdMTM(OptProb, nIter, alpha0, hyperFun):

    u = OptProb.randSol()
    z = 0*u
    stats = np.zeros( [nIter, OptProb.Nstats] )

    for k in range(nIter):

        g     = OptProb.gradFun(u)

        alpha = hyperFun.SS(u, alpha0, k, g)

        z     = hyperFun.mtmGamma*z - alpha*g

        u = u + z

        stats[k,:] = OptProb.computeStats(u, alpha, k, g)

        OptProb.printStats(k, nIter, stats)

    return u, stats

Nesterov

Highlighted lines point out the differences between GD and Nesterov [Nes83].

def hosgdNTRV(OptProb, nIter, alpha0, hyperFun):

    u1 = OptProb.randSol()
    y  = u1.copy()

    stats = np.zeros( [nIter, OptProb.Nstats] )

    for k in range(nIter):

        g     = OptProb.gradFun(y)

        alpha = hyperFun.SS(u1, alpha0, k, g)
        gamma = hyperFun.ISeq(k)

        u0 = u1.copy()

        u1 = y - alpha*g

        y     = u1 + gamma*(u1 - u0)


        stats[k,:] = OptProb.computeStats(u1, alpha, k, g)

        OptProb.printStats(k, nIter, stats)

    return u1, stats

Parameters

def hosgdMTM(OptProb, nIter, alpha0, hyperFun):

def hosgdNTRV(OptProb, nIter, alpha0, hyperFun):

OptProb

Blah, blah

nIter

Total number of iterations.

alpha0

Initial step-size.

hyperFun

Blah, blah

---

Simulation

1. Generate input data

    import numpy as np

    # --- Data generation (N,M: user inputs)
    # --------------------------------------
    rng = np.random.default_rng()

    A = rng.normal(size=[N,M])
    D = np.sqrt(max(N,M))*np.diag( rng.random([max(N,M),]), 0)
    A += D[0:N,0:M]
    A /= np.linalg.norm(A,axis=0)

    xOrig = np.random.randn(M,1)

    b = A.dot(xOrig) + sigma*np.random.randn(N,1)

2. Load the optimization problem

    # --- Optimization model
    # --- (see "Parameters", "OptProb", "E.g. quadratic func."
    #      in the tabbed panel above)
    # ---------------------------------------------------------

    OptProb = hosgdFunQlin(A,b)

3. Select the hyper-parameters routines

    # --- It is assumed that class 'ss' is defined
    #     in file 'HoSGDdefs.py'
    # --- (see "Parameters", "hyperFun", "class ss"
    #      in the tabbed panel above)
    # ---------------------------------------------------------

    import HoSGDdefs as hosgdDef


    # --- hyperPars
    # --- (see "Parameters", "hyperFun", "E.g."
    #      in the tabbed panel above)
    # ---------------------------------------------------------

    # Momentum case:
    hyperPmtm = hosgdHyperFun(OptProb, ssPolicy=hosgdDef.ss.Cte, mtmGamma=0.9)

    # Nesterov case:
    hyperPntrv = hosgdHyperFun(OptProb, ssPolicy=hosgdDef.ss.Cte, iseqPolicy=hosgdDef.iseq.Ntrv)

4. Execute Momentum or Nesterov

    # --- nIter, alpha0: user defined.
    # --- OptProb: see #2 in the current list
    # --- hyperP: see #3 in the current list

    # Momentum case:
    u1, stats1 = hosgdMTM(OptProb, nIter, alpha0, hyperPmtm)

    # Nesterov case:
    u2, stats2 = hosgdNTRV(OptProb, nIter, alpha0, hyperPntrv)

---

Full solution

HoSGDdefs.py

from enum import Enum, IntEnum, unique

@unique
class ss(Enum):
  Cte            = (0, 'Cte step-size')
  Cauchy         = (1, 'Cauchy')
  CauchyLagged   = (2, 'Cauchy-BB (lagged)')
  CauchyRand     = (3, 'Cauchy rand')
  CauchySupp     = (4, 'Cauchy supp')
  CauchyLSupp    = (5, 'Cauchy-BB supp')
  BBv1           = (6, 'BBv1')
  BBv2           = (7, 'BBv2')
  BBv3           = (8, 'BBv3')

  def __init__(self, val, txt):
      self.val  = val
      self.txt  = txt

  @classmethod
  def printSS(cls):
      for k in cls:
        print('ss.{}:'.format(k.name), k.val, k.txt)

@unique
class iseq(Enum):
  Ntrv           = (0, 'Standard ISeq')
  Lin            = (1, 'Linear ISeq')
  GLin           = (1, 'Generalized linear ISeq')

  def __init__(self, val, txt):
      self.val  = val
      self.txt  = txt

  @classmethod
  def printLR(cls):
      for k in cls:
        print('iseq.{}:'.format(k.name), k.val, k.txt)

HoSGDL2agd.py

import numpy as np
import scipy as sc
from scipy import signal

import matplotlib.pylab as PLT

import HoSGDdefs as hosgdDef

from HoSGDlabGD import hosgdFunQlin, hosgdHyperFun, hosgdGD, plotGDDictStats


class hosgdHyperFunAGD(hosgdHyperFun):
    r"""Class (child) related to routines associated to hyperPars computation
    """

    def __init__(self, OptProb, ssPolicy=hosgdDef.ss.Cte, iseqPolicy=hosgdDef.iseq.Ntrv, mtmGamma=0.9, iseqPar1=2,iseqPar2=80):
        self.ssPolicy = ssPolicy
        self.iseqPolicy = iseqPolicy
        self.fwOp = OptProb.fwOp
        self.SS   = self.sel_SS()
        self.ISeq = self.sel_ISeq()
        self.mtmGamma = mtmGamma
        self.iseqPar1 = iseqPar1
        self.iseqPar2 = iseqPar2

    # --- === ---
          hosgdDef.iseq.Ntrv.val:   self.iseqNtrv,
          hosgdDef.iseq.Lin.val:    self.iseqLin,
          hosgdDef.iseq.GLin.val:   self.iseqGlin,
          }

      iseqFun = switcher.get(self.iseqPolicy.val, "nothing")

      func = lambda k: iseqFun(k)

      return func

    # --- === ---

    def iseqNtrv(self, k):

        if k == 0:
           self.t0 = 1.0

        self.t1 = 0.5 * float(1. + np.sqrt(1. + 4. * self.t0**2.))
        gamma = (self.t0-1.)/self.t1
        self.t0 = self.t1

        return gamma


    def iseqLin(self, k):

        gamma = ((k+1.)-1.)/( ((k+1.)-1.) + self.iseqPar1 + 1)

        return gamma


    def iseqGlin(self, k):

        gamma = ((k+1.)-1. -(1+self.iseqPar1) + self.iseqPar2 )/((k+1.) + self.iseqPar1  )

        return gamma



def hosgdMTM(OptProb, nIter, alpha0, hyperFun):

    u = OptProb.randSol()
    z = 0*u
    stats = np.zeros( [nIter, OptProb.Nstats] )

    for k in range(nIter):

        g     = OptProb.gradFun(u)

        alpha = hyperFun.SS(u, alpha0, k, g)

        z     = hyperFun.mtmGamma*z - alpha*g

        u = u + z

        stats[k,:] = OptProb.computeStats(u, alpha, k, g)

        OptProb.printStats(k, nIter, stats)

    return u, stats

# ===========================================

def hosgdNTRV(OptProb, nIter, alpha0, hyperFun):

    u1 = OptProb.randSol()
    y  = u1.copy()

    stats = np.zeros( [nIter, OptProb.Nstats] )

    for k in range(nIter):

        g     = OptProb.gradFun(y)

        alpha = hyperFun.SS(u1, alpha0, k, g)
        gamma = hyperFun.ISeq(k)

        u0 = u1.copy()

        u1 = y - alpha*g

        y     = u1 + gamma*(u1 - u0)


        stats[k,:] = OptProb.computeStats(u1, alpha, k, g)

        OptProb.printStats(k, nIter, stats)

    return u1, stats

# ===========================================


def exQlinAGD(nIter, alpha, N=1000, M=500, sigma=0.05, ssPolicy=hosgdDef.ss.Cte, iseqPolicy=None, mtmGamma=None):

    # Examples
    #

    # --- Data generation
    # -------------------
    rng = np.random.default_rng()

    A = rng.normal(size=[N,M])
    D = np.sqrt(max(N,M))*np.diag( rng.random([max(N,M),]), 0)
    A += D[0:N,0:M]
    A /= np.linalg.norm(A,axis=0)

    xOrig = np.random.randn(M,1)

    b = A.dot(xOrig) + sigma*np.random.randn(N,1)

    # --- Optimization model
    # ----------------------

    OptProb = hosgdFunQlin(A,b)

    # --- HyperPar
    # ------------

    if iseqPolicy is None and mtmGamma is None:

        u = []
        stats = []
        ssPlcyList = []
        algoList = []

        # --- ___ ---

        hyperP = hosgdHyperFun(OptProb, ssPolicy=ssPolicy)

        sol = hosgdGD(OptProb, nIter, alpha, hyperP)
        u.append(sol[0])
        stats.append(sol[1])
        ssPlcyList.append( ssPolicy )
        algoList.append('GD')

        # --- ___ ---

        hyperP = hosgdHyperFunAGD(OptProb, ssPolicy=ssPolicy, mtmGamma=0.9)

        sol = hosgdMTM(OptProb, nIter, alpha, hyperP)
        u.append(sol[0])
        stats.append(sol[1])
        ssPlcyList.append( ssPolicy )
        algoList.append('Momentum')

        # --- ___ ---

        hyperP = hosgdHyperFunAGD(OptProb, ssPolicy=ssPolicy, mtmGamma=0.9)

        sol = hosgdNTRV(OptProb, nIter, alpha, hyperP)
        u.append(sol[0])
        stats.append(sol[1])
        ssPlcyList.append( ssPolicy )
        algoList.append('Nesterov')


        stDict = {'stats': stats, 'ssPlcy': ssPlcyList, 'alphaVal': alpha, 'algoList': algoList, 'alphaPlot':False}

        plotAGDDictStats(stDict)

    elif iseqPolicy is None and mtmGamma is not None:

        u = []
        stats = []
        ssPlcyList = []
        algoList = []

        hyperP = hosgdHyperFunAGD(OptProb, ssPolicy=ssPolicy, mtmGamma=mtmGamma)

        sol = hosgdMTM(OptProb, nIter, alpha, hyperP)
        u.append(sol[0])
        stats.append(sol[1])
        ssPlcyList.append( ssPolicy )
        algoList.append('Momentum')

        stDict = {'stats': stats, 'ssPlcy': ssPlcyList, 'alphaVal': alpha, 'algoList': algoList, 'alphaPlot':False}

        plotAGDDictStats(stDict)

    elif iseqPolicy is not None and mtmGamma is None:

        u = []
        stats = []
        ssPlcyList = []
        algoList = []

        hyperP = hosgdHyperFunAGD(OptProb, ssPolicy=ssPolicy, iseqPolicy=iseqPolicy)

        sol = hosgdNTRV(OptProb, nIter, alpha, hyperP)
        u.append(sol[0])
        stats.append(sol[1])
        ssPlcyList.append( ssPolicy )
        algoList.append('Nesterov')


        stDict = {'stats': stats, 'ssPlcy': ssPlcyList, 'alphaVal': alpha, 'algoList': algoList, 'alphaPlot':False}

        plotAGDDictStats(stDict)

    return u, stats



def plotAGDDictStats(stDict):


  stats    = stDict.get('stats')
  ssPlcy   = stDict.get('ssPlcy')
  alpha    = stDict.get('alphaVal')
  algoName = stDict.get('algoList')

  alphaPlot  = stDict.get('alphaPlot')

  # --- Plot cost function ---
  PLT.figure()

  for n in range(len(stats)):
    PLT.semilogy(stats[n][:,1], label=r'$\alpha_k$ : {0} -- {1}, {2}'.format(alpha, algoName[n], ssPlcy[n].txt) )

  PLT.legend(loc='upper right')
  PLT.ylabel(r'$f(x) = \frac{1}{2}\| A \mathbf{x} - \mathbf{b} \|_2^2$', fontsize=16)
  PLT.xlabel('Iteration', fontsize=16)
  PLT.title('Cost functional',fontsize=16)

  # --- Plot SS ---
  if alphaPlot:

    PLT.figure()

    for n in range(len(stats)):
      PLT.plot(stats[n][1::,2], label=r'$\alpha_k$ : {0}'.format(ssPlcy[n].txt) )

    PLT.legend(loc='upper right')
    PLT.ylabel(r'$\alpha$', fontsize=20)
    PLT.xlabel('Iteration', fontsize=16)
    PLT.title('Step-size',fontsize=16)

  # ---

  PLT.show()

Simple Simulation

import numpy as np
import HoSGDlabAGD as H
import HoSGDdefs as hosgdDef

# run defualt sim: compare GD, MTM and NTRV

u, st = H.exQlinAGD(40, 0.01, N=500, M=2000)