Hidden layer / ELM
Considering a cost functional with the same characteristics as the one used for the SGD case, then
Modify the Softmax specialization of the hosgdOptProb class so as to:
It accepts an optimization problem which includes a hidden layer (not trainable)
Add different activation functions, e.g. ReLU, ELU, etc.
Previously, the Softmax function (for a full explanation see Lecture 3b’s introduction) has been written as:
where
\(\mathbf{X} = [ \mathbf{x}_1, \mathbf{x}_2, \ldots, \mathbf{x}_N ] \in \mathbb{R}^{r_0 \times N}\) represents the training dataset.
\(\mathbf{W} \in \mathbb{R}^{r_0 \times L}\) represents the weights (to be trained); furthermore, \(\mathbf{w}_l\), the \(l^{th}\)-column of matrix \(\mathbf{W}\), is associated with \(l^{th}\)-class of the classification problem.
\(L\) is the number of classes associated with the datatset \(\mathbf{X}\).
\(\mathbf{w}_{_{\mathbf{\cal{L}}_n}}\): knowing that the input data \(\mathbf{x}_n\) is class \({\mathbf{\cal{L}}}_n\), then \(\mathbf{w}_{_{\mathbf{\cal{L}}_n}}\) represents the corresponding column in matrix \(\mathbf{W}\).
For this particular simulation, first let (1) be written as
where
\(\mathbf{c}_n^{^{(\mathbf{x})}}\) represents a canonical vector (value one at position \(n\), zero elsewhere) of length \(\mathbf{X}.\mbox{shape}[1]\)
\(\mathbf{c}_l\) represents a canonical vector of length L
\(\mathbf{h}_n \in \mathbb{R}^L\) is the one-hot representation of \(\mathbf{x}_n\)’s class.
Then, by considering \(\mathbf{Z}_0 = \mathbf{X}\) and \(\mathbf{Z}_1 = \varphi_1(\mathbf{W_0}\mathbf{Z}_0)\), (2) can be written as (3), which in turn may be interpreted as the Softmax function along with a non-trainable hidden layer (which amounts to a particular example of ELM [HCS06] ) :
where
\(\varphi_1(\cdot)\) is a non-linear activation function.
\(\mathbf{Z_0} \in \mathbb{R}^{r_0 \times N}\)
\(\mathbf{W_0} \in \mathbb{R}^{r_1 \times r_0}:\mbox{ random value matrix} \qquad \color{darkgray} \mbox{note that } \mathbf{Z}_1 = \varphi_1(\mathbf{W_0}\mathbf{Z}_0) \in \mathbb{R}^{r_1 \times N}\)
\(\mathbf{W_1} \in \mathbb{R}^{r_1 \times L}\)
\(r_1 \ll r_0 \)
class hosgdFunSoftMax(hosgdOptProb):
r""" F(W) = (1/N) \sum_n f_n(W)
f_n(W) = < Xn, Wl_n > + log( \sum_l e^{ -< Xl, Wl >} )
"""
def __init__(self, X, Y, nClass, Xtest=None, Ytest=None, lmbd=0,
gNormOrd=2, Nstats=5, verbose=10, initSol=None):
self.X = X
self.Y = Y
self.nClass = nClass
self.Xtest = Xtest
self.Ytest = Ytest
self.lmbd = lmbd
self.Nstats = Nstats
self.gNormOrd = gNormOrd
self.verbose = verbose
self.initSol = initSol # if not None --> reproducible initial solution
# ---------
def costFun(self, W):
fCost = np.sum(np.log(np.sum(np.exp(-self.X.transpose().dot(W)), axis=1)))
fCost += np.sum( self.X*W[:,self.Y] )
fCost /= float(self.X.shape[1])
if self.lmbd > 0:
fCost += self.lmbd*(sum( np.power(W.ravel(),2) ))/float(self.X.shape[1])
return fCost
# ---------
def fwOp(self, W):
return None
# ---------
def gradFun(self, W, n):
z = self.X[:,np.ix_(n)].squeeze(1) # select batch elements
g = -z.dot( softmax(-z.transpose().dot(W),axis=1) )
for k in range(len(n)):
g[:,self.Y[n[k]] ] += z[:,k]
g /= float(len(n))
if self.lmbd > 0:
g += self.lmbd*W
return g
# ---------
def randSol(self):
if self.initSol is None:
rng = np.random.default_rng()
else:
rng = np.random.default_rng(self.initSol)
return 0.01*rng.normal(size=[self.X.shape[0], self.nClass] )
# ---------
def computeStats(self, W, alpha, k, g):
cost = self.costFun(W)
gNorm = self.gradNorm(g, self.gNormOrd)
success = self.computeSuccess(W)
return np.array([k, cost, alpha, gNorm, success])
# ---------
def computeSuccess(self, W):
if self.Xtest is not None and self.Ytest is not None:
classVal = -np.matmul(self.Xtest.transpose(), W)
success = sum( np.argmax(classVal,axis=1) == self.Ytest )
return float(success)/float(self.Xtest.shape[1])
else:
return None
# ---------
def printStats(self, k, nEpoch, v):
if k == 0:
print('\n')
if self.verbose > 0:
if np.remainder(k,self.verbose)==0 or k==nEpoch-1:
if v[k,4] is None:
print('{:>3d}\t {:.3e}\t {:.2e} {:.2e}'.format(int(v[k,0]),v[k,1],v[k,2],v[k,3]))
else:
print('{:>3d}\t {:.3e}\t {:.2e} {:.2e}\n \t \
success rate (training): {:.3e}'.format(int(v[k,0]),v[k,1],v[k,2],v[k,3],v[k,4]))
return
# ---------
def gradNorm(self, g, ord=2):
if g is None:
return -1.0
if ord == 2:
return np.linalg.norm(g.ravel(),ord=ord)**ord
else:
return np.linalg.norm(g.ravel(),ord=ord)
\( \begin{array}{llcl} \bullet & \phi(u) & = & \max \{ u,\, 0 \} \\ \bullet & \frac{\partial \phi(u)}{\partial u} & = & \psi(u) = 1.*(u>0) \end{array} \)
Python code
import numpy as np
def afReLu(u, flag):
if flag is False:
return np.maximum(u,0)
else:
return 1.*(u>0)
\( \begin{array}{llcl} \bullet & \phi(u,\tau) & = & \max \{ u,\, 0 \} + \tau\cdot\min\{ \mbox{e}^{u}-1, 0 \} \\ \bullet & \frac{\partial \phi(u)}{\partial u} & = & \psi(u) = 1.*(u>0) + \tau.*(u<0)*\mbox{e}^{u} \end{array} \)
Python code
import numpy as np
def afELU(u, flag, par1=None):
if par1 is None:
par1 = 0.5
if flag is False:
return np.maximum(u,0) + par1*np.min( np.exp(u)-1, 0 )
else:
return 1.*(u>0) + par1*(u<0)*(np.exp(u))
Proposed solution
Among other pausible solutions, here a very simple but not scalable (hidden layers point of view) is listed. A more elaborate solution is the one used along with the Backpropagation simulation.
Highlighted lines point out the key idea behind this soution: transform the input dataset, using the
HL classto that end, and treat it as the original one.The
hosgdFunELMSoftMaxclass is identical to thehosgdFunSoftMaxsaved for the part shown below.
class hosgdFunELMSoftMax(hosgdOptProb):
r""" F(W) = (1/N) \sum_n f_n(Z)
f_n(W) = < Zn, Wl_n > + log( \sum_l e^{ -< Zl, Wl >} )
"""
def __init__(self, X, Y, nClass, HL, Xtest=None, Ytest=None, lmbd=0,
gNormOrd=2, Nstats=5, verbose=10, initSol=None):
self.Xorig = X
self.Y = Y
self.nClass = nClass
self.Xorigtest = Xtest
self.Ytest = Ytest
self.lmbd = lmbd
self.Nstats = Nstats
self.gNormOrd = gNormOrd
self.verbose = verbose
self.initSol = initSol # if not None --> reproducible initial solution
#
self.HL = HL
self.X = self.HL.fwd( self.Xorig )
self.Xtest = self.HL.fwd( self.Xorigtest )
# ---------
class hosgdFunHL(object):
def __init__(self, hlRows=-1, hlFun=hosgdDef.hlFun.dense, actFun=None, par1=None, par2=None):
self.par1 = par1
self.par2 = par2
self.hlFun = hlFun
self.hlRows = hlRows
self.Adense = None
self.AFclass = hosgdFunAF(actFun=actFun, par1=par1, par2=par2)
self.actFun = self.AFclass.sel_AF()
self.sel_HL()
def sel_HL(self):
switcher = {
hosgdDef.hlFun.dense.val: self.hlDense,
}
hlFun = switcher.get(self.hlFun.val, "nothing")
self.fwd = lambda u: hlFun(u)
return
# --- === ---
def hlDenseInit(self, Xorig):
rng = np.random.default_rng()
if self.hlRows == -1:
self.Adense = rng.normal(size=[int(Xorig.shape[0]/2), Xorig.shape[0]] )
else:
self.Adense = rng.normal(size=[self.hlRows, Xorig.shape[0]] )
self.Adense /= np.linalg.norm(self.Adense, axis=0)
def hlDense(self, u ):
if self.Adense is None:
self.hlDenseInit(u)
return self.actFun( self.Adense.dot(u), False )
class hosgdFunAF(object):
def __init__(self, actFun, par1=None, par2=None):
self.actFun = actFun
self.par1 = par1
self.par2 = par2
def sel_AF(self):
switcher = {
hosgdDef.actFun.ReLU.val: self.afReLu,
hosgdDef.actFun.RReLU.val: self.afRReLu,
hosgdDef.actFun.ELU.val: self.afELU,
}
if self.actFun is None:
afFun = self.afIdentity
else:
afFun = switcher.get(self.actFun.val, None)
func = lambda u,flag: afFun(u,flag)
return func
# --- === ---
def afIdentity(self, u, flag):
return u
# --- === ---
def afReLu(self, u, flag):
if flag is False:
return np.maximum(u,0)
else:
return 1.*(u>0)
# --- === ---
def afRReLu(self, u, flag):
pass
# --- === ---
def afELU(self, u, flag):
if self.par1 is None:
self.par1 = 0.5
if flag is False:
return np.maximum(u,0) + self.par1*np.min( np.exp(u)-1,0)
else:
return 1.*(u>0) + self.par1*(u<0)*(np.exp(u))
Full solution
HoSGDlabAF.py
import numpy as np
import scipy as sc
from scipy import signal
from scipy.special import softmax,logsumexp
import matplotlib.pylab as PLT
from matplotlib.ticker import MaxNLocator
import HoSGDdefs as hosgdDef
from HoSGDdefs import hosgdOptProb
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2' # Disbales TF's warnings (they don' shown in generated HTML)
# Note: TF is used to have a simple access to MNIST
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras.datasets import mnist
from tensorflow.keras.datasets import cifar10
from HoSGDlabSGD import hosgdFunSoftMax, hosgdHyperFunSGD, hosgdSGD, stdPreproc
from HoSGDlabSGDVariants import hosgdMTM, hosgdRMSProp, hosgdADAM, plotSGDStatsList
Routines to execute example and plot results
def exMultiClass(nEpoch, blkSize, alpha, dataset='mnist', lrPolicy=hosgdDef.lrSGD.Cte, lrSDecay=20, lrTau = 0.5, verbose=5):
# Examples
# w, stats = exMultiClass(40, 128, 0.025, dataset='cifar10',verbose=20)
# --- Load data
# -------------------
flagDataset = False
if dataset.lower() == 'mnist':
(X, Y), (Xtest, Ytest) = mnist.load_data()
flagDataset = True
if dataset.lower() == 'cifar10':
(X, Y), (Xtest, Ytest) = cifar10.load_data()
flagDataset = True
if flagDataset is False:
print('Dataset {} is no valid'.format(dataset))
return
if verbose == 1:
print('Shape (training data):', X.shape)
print('Shape (valid/testing data):', Xtest.shape)
print('\n')
# pre-processing
X = stdPreproc(X)
Xtest = stdPreproc(Xtest)
# Data vectorization
X = np.transpose( X.reshape(X.shape[0], np.array(X.shape[1::]).prod()) )
Xtest = np.transpose( Xtest.reshape(Xtest.shape[0], np.array(Xtest.shape[1::]).prod()) )
Y = Y.ravel()
Ytest = Ytest.ravel()
# --- Optimization model
# ----------------------
OptProb = hosgdFunSoftMax(X, Y, 10, verbose=verbose, Xtest=Xtest, Ytest=Ytest)
# --- Hidden Layer (not trainable --> ELM)
# ----------------------
elmId = hosgdFunHL(hlRows=512, actFun=None)
elmReLU = hosgdFunHL(hlRows=512, actFun=hosgdDef.actFun.ReLU)
elmELU = hosgdFunHL(hlRows=512, actFun=hosgdDef.actFun.ELU)
elmIOptProb = hosgdFunELMSoftMax(X, Y, 10, elmId, verbose=verbose, Xtest=Xtest, Ytest=Ytest)
elmReLUOptProb = hosgdFunELMSoftMax(X, Y, 10, elmReLU, verbose=verbose, Xtest=Xtest, Ytest=Ytest)
elmELUOptProb = hosgdFunELMSoftMax(X, Y, 10, elmELU, verbose=verbose, Xtest=Xtest, Ytest=Ytest)
# --- HyperPar (this is kept in order to have a similar structure to the SD case (see Lab 1a)
# ------------
hyperP = hosgdHyperFunSGD(lrPolicy=lrPolicy, lrSDecay=lrSDecay, lrTau=lrTau)
W = []
stats = []
nameVar = []
# --- Call SGD
# -----------
sol = hosgdSGD(OptProb, nEpoch, blkSize, alpha, hyperP)
W.append(sol[0])
stats.append(sol[1])
nameVar.append('SGD')
# --- Call SGD+linear hidden layer
# -----------
sol = hosgdSGD(elmIOptProb, nEpoch, blkSize, alpha, hyperP)
W.append(sol[0])
stats.append(sol[1])
nameVar.append('SGD -- Linear HL')
# --- Call SGD+ELM+ReLU
# -----------
sol = hosgdSGD(elmReLUOptProb, nEpoch, blkSize, alpha, hyperP)
W.append(sol[0])
stats.append(sol[1])
nameVar.append('SGD -- ELM, ReLU')
# --- Call SGD+ELM+ELU
# -----------
sol = hosgdSGD(elmELUOptProb, nEpoch, blkSize, alpha, hyperP)
W.append(sol[0])
stats.append(sol[1])
nameVar.append('SGD -- ELM, ELU')
# --- Plot results
# ----------------
plotSGDStatsList(stats, nameVar)
return W, stats
def plotSGDStatsList(stats,nameVar):
# --- Plot results ---
L = len(stats)
ax = PLT.figure().gca()
ax.xaxis.set_major_locator(MaxNLocator(integer=True))
for k in range(L):
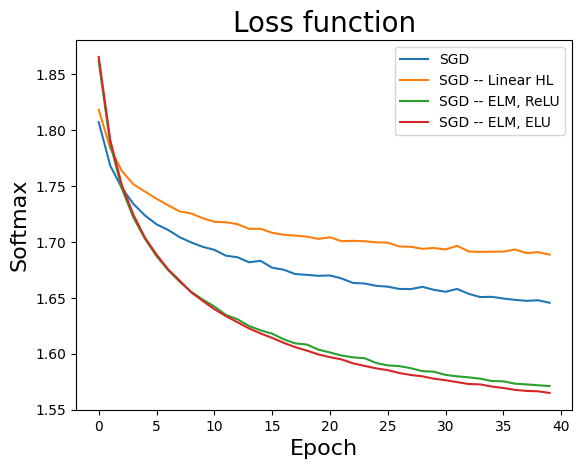
PLT.plot(stats[k][:,1], label=r'{0}'.format(nameVar[k]) )
PLT.legend(loc='upper right')
PLT.ylabel('Softmax', fontsize=16)
PLT.xlabel('Epoch', fontsize=16)
PLT.title('Loss function', fontsize=20)
if stats[0][0,4] is not None:
ax = PLT.figure().gca()
ax.xaxis.set_major_locator(MaxNLocator(integer=True))
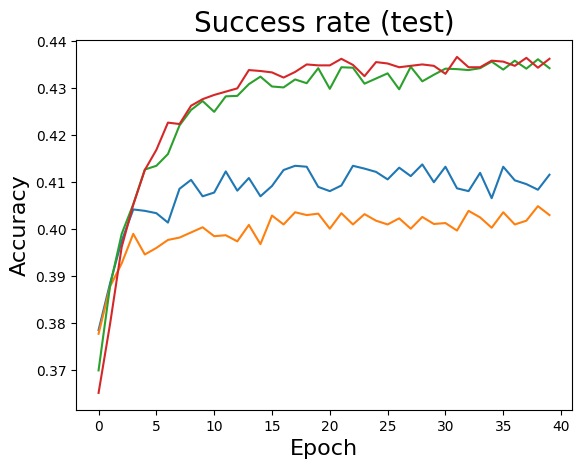
for k in range(L):
PLT.plot(stats[k][:,4] )
PLT.ylabel('Accuracy', fontsize=16)
PLT.xlabel('Epoch', fontsize=16)
PLT.title('Success rate (test)', fontsize=20)
PLT.show()
Simple Simulation (CIFAR-10)
import HoSGDlabAF as HAF
sol = HAF.exMultiClass(40, 128, 0.025, dataset='cifar10',verbose=-1)